Executive Summary
Following the third inter-Korean summit in Pyongyang, there has been much discussion surrounding the possible denuclearization of North Korea. However, it remains to be seen if any tangible progress can be made towards ‘final, fully-verified denuclearization.’ At the time of writing, it was difficult to predict even if a tentative agreement could be reached to allow nuclear inspectors into North Korea to examine and verify the denuclearization process. Against this backdrop, we have jumped ahead in time to focus our research on measuring the effectiveness of nuclear inspection in North Korea. In particular, we are interested in determining the probability of detecting violations assuming North Korea is not abiding by international law. The specifics of violation will be context-dependent. In our research, it was assumed from the outset that only a ‘limited number’ of nuclear / WMD sites could be accessed by inspectors.
Essentially, we are interested in the probability of detecting at least one violation because one violation will constitute sufficient evidence that North Korea is again deceiving the international community. Our probability threshold is set at 90% throughout this research. But the choice of threshold is quite arbitrary. Our threshold has been carefully chosen to ensure that it is unlikely for a violation committed to go unnoticed. It is also assumed that each nuclear / WMD site is given an equal chance of committing a violation as it is difficult to collect intelligence on North Korea. This is the simplest assumption that can be made. We have provided the minimum number of inspections required to attain our threshold in each of examples used which include the Yongbyon nuclear complex, the critical and secondary nuclear / WMD sites and North Korea’s underground facilities.
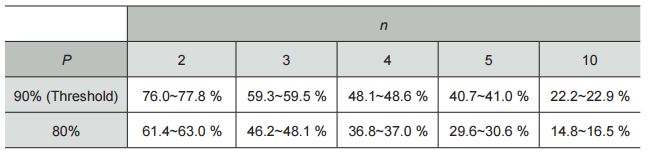
In Chapter 5, our findings are summarized in three tables. Using these tables, one can calculate the approximate minimum number of inspections required for a given number of sites, N. One of the tables is shown below.
The number of inspections required for P as a percentage of N when p = 0.91
(N used: 27~14,000)
This process enables ‘back of the envelope calculations’ to ensure that one can get an immediate sense of the magnitude of the task at hand. In the case of North Korea’s Yongbyon nuclear complex, there are approximately 400 buildings (i.e., N = 400). A violation here can mean hiding fissile materials. Once it is assumed that there are 5 sites in violation (i.e., n = 5) among 400 sites (or buildings), then a minimum of 164 sites would need to be inspected to meet our threshold (i.e., P = 90%).
In reality, it is highly unlikely for North Korea to risk committing a violation at the Yongbyon nuclear complex since it has indicated its willingness to permanently shut down the nuclear complex in return for corresponding actions from Washington as spelt out in the Pyongyang Joint Declaration. Therefore, it is necessary to carry out inspections at various sites beyond the Yongbyun nuclear complex.
According to the research conducted by Kristensen and Norris published in Bulletin of the Atomic Scientist, North Korea may have assembled 10~20 nuclear weapons. In terms of relevance to our study, suppose that there are 10 sites in violation. Here, a violation can mean hiding, on average, one or two nuclear weapons in each site corresponding to a total of 10 or 20 nuclear weapons respectively. From North Korea’s perspective, there will be a trade-off between a need to minimize the risk of being detected by storing its nuclear weapons in fewer sites as possible and a need to store its nuclear weapons in multiple sites to minimize the risk of all of its nuclear weapons being detected. North Korea is unlikely to put all its eggs in one basket and moving these nuclear weapons will increase the probability of being detected while in transit.
Now, once it is assumed that these 10 sites (i.e., facilities) are among North Korea’s 14,000 underground facilities (see section 4.4), then a minimum of approximately 3,206 sites would need to be inspected to meet our threshold.
As the examples illustrate, this table is very useful in approximating the minimum number of inspections required. In all tables, the number of sites in violation, n, is deliberately assumed to be fairly low2 (i.e., n: 2~5) while P is set quite high at both 90% (threshold) and 80% levels. Since this approach only provides a quick but approximate estimate on the minimum number of inspections required, one can always turn to Monte Carlo simulations to determine a more accurate estimate. The methodological details can be found in the appendix. Now, if no violation is found at the 90% threshold, then it will significantly reassure us that North Korea is abiding by international law / agreements. Of course, one needs to have a priori estimate on the number of sites in violation. This will be based on intelligence and an educated guess.
It must be borne in mind that we have only considered some aspects of inspection based on probability theory in this report. It goes without saying that good detective skills rooted in science and technology are required of inspectors to carry out their duties effectively.
Table of Contents
-Executive Summary
-1. Introduction
-2. North Korea’s Nuclear / WMD facilities
-3. The Descriptions of Mathematical Models (Analytical & Monte Carlo)
-4. Simulation Findings
-5. Quick Estimation of m, the number of inspections required
-6. Conclusion
-Appendix – Inspection Violation (Confidence) Model

 Facebook
Facebook Twitter
Twitter