Introduction
Since the inter-Korean summit and the U.S.-North Korea summit this year, many questions are being asked about how North Korea is going to implement the ‘complete’ denuclearization of the Korean peninsula to which it is said to have committed. However, in the past, this position was held by North Korea as a deliberate time-wasting ploy to continue their nuclear weapons development.
If North Korea truly wants the lifting of international sanctions and economic cooperation from the international community, ‘complete’ denuclearization must truly be complete. ‘Complete’ (or ‘Fully-Verified’1 as used by a U.S. State Department spokeswoman recently) denuclearization necessitates proper inspection and verification – even then verifying ‘complete’ denuclearization is not attainable. Despite this shortcoming, carrying out proper inspection and verification is far easier said than done. To give an example, if there is a suspicious site in Iran, the inspection process involves requesting for clarification / access / dispute resolution / implementation, which can take up to 24 days. If a resolution is still not reached by the implementation stage, then the Joint Commission2 can invoke a separate dispute resolution process potentially adding yet another 30 days.3 In total, 54 days could elapse before an inspector can set foot in the suspicious site. There is plenty of time to get rid of any incriminating evidence, and the element of surprise which is crucial in inspection is completely missing. Obviously, this raises doubts as to whether meaningful inspection and verification can ever be carried out over North Korea’s nuclear sites. According to a 2014 RAND report,4 there are 141 WMD sites in North Korea. One of them, Yongbyon nuclear complex, is estimated to have some 3905 to 6636 buildings alone depending on the source. North Korea’s nuclear and missile programs are much more advanced and extensive than those of Iraq, Libya or Iran. According to Joseph Bermudez, the author of three books on the North Korean military, North Korea has 11,000-14,000 underground facilities. Stockpiles of biological, chemical or nuclear weapons could be easily hidden away in any one of these, and they could house a production line for producing highly-enriched uranium. The scale of the problem faced by inspectors is immense and unprecedented. The International Atomic Energy Agency (IAEA) has 300 inspectors.7 The large number of facilities poses a daunting challenge let alone all barriers and impediments North Koreans are likely to put up.
The term ‘Complete’ in ‘Complete, Verifiable and Irreversible Dismantlement’ is a misnomer. A degree of assurance is perhaps a better description. One of the most important functions of an inspection system is to provide this assurance that North Korea is keeping its agreements. However, it is virtually impossible to discard the possibility that some nuclear warheads are hidden. U.S. Secretary of State Mike Pompeo once said that ‘major’ North Korean nuclear disarmament can be satisfactorily achieved in two and a half years. It remains to be seen if this can be achieved. The latest U.S. intelligence assessment points to the contrary, saying that North Korea was increasing its production of enriched uranium even as it was engaged in diplomacy with the United States.8
There has been much talk of inspection, but our focus is to quantify its effectiveness on North Korea’s nuclear sites – if certain rather restricting conditions are met in the form of mathematical inequalities. We want to determine what our chances are of detecting any violation assuming North Korea is cheating. Specifically, how many inspections are required and how confident should the inspectors be to improve these chances of detection to 80% or 90%, for instance? These quantities can be probabilistically determined through the adoption of a mathematical model. The situation envisaged and modeled describes groups of international inspectors allowed to access only a limited number of North Korea’s nuclear sites out of many sites simultaneously. Each of these sites is given an equal chance of committing a violation. This is the simplest assumption. Therefore, if particular sites are suspected with good reason to have committed violations, then the chances of detecting any violation should be greater than the one on which our calculations are based.9 In other words, our calculations could provide baseline estimates. Besides, the inspectors and North Korean authorities are going to outguess each other on a game of cat and mouse, thence the assigning of the equal chance.
The fixed (limited) number of inspections is assumed on the grounds that North Korean authorities are unlikely to give the inspectors total freedom to check on any number of nuclear sites or that the IAEA does not have enough manpower necessary to carry out a thorough inspection of the whole complex. In the following section, Yongbyon’s facilities are used as an example to show how our chances of detecting North Korea’s violations change under different simulation settings. In the process, the minimum number of inspections required to increase our chances above a certain threshold (e.g., 90%) can be estimated for a given simulation setting. The choice of Yongbyon’s facilities is quite arbitrary. It can be extended to include 11,000-14,000 underground facilities mentioned above.10 The mathematical details are explained in the appendix for those more technically oriented.
Simulation findings
At North Korea’s Yongbyon nuclear complex, there are approximately 400 buildings (N).11 Every one of these buildings is a potential target for inspection. We are ultimately interested in determining P, the probability of detecting at least one violation assuming that North Korea is cheating. The higher the value of P, the more likely that we will catch North Koreans red-handed. The factors that determine P are the number of sites in violation (n), the number of inspections allowed (m) and the probability of correctly identifying a violation by the inspectors assuming that they are at a violating site (p). The exact mathematical equation for and the conditions under which it can be used are explained in detail in the appendix.
The following simulation settings are chosen to see how P ‘evolves’ with different values of n,m and p.12 For n which is unknown to us, we have chosen the values 20, 40, 60, 80 which correspond to 5%, 10%, 15%, 20% of N. North Koreans will make n as small as possible.13 For each fixed n, five different values14 of m corresponding to 20%, 40%, 60%, 80% and 100% of n have been chosen. For p, the range of values from 0.4 to 0.9 are used. One of the mathematical conditions demands that the number of inspections, m, be less than equal to the number of sites in violation, n (see footnote 18). Figure 1 below shows P, the probability of detecting at least one violation, with different values of n,m and p.
Figure 1. Probability of detecting one or more violations with different n,m and p
Consider the top-left graph with 20 buildings in violation among 400 buildings. Suppose that only 4 inspections are allowed and the probability of correctly identifying a violation is 0.7. Then, the equation informs us that there is only a 13% probability of detecting at least one violation. This improves to 17% when the probability of correctly identifying a violation becomes 0.9. When the number of inspections increases to 20, then P improves to 52% and 61% with p fixed at 0.7 and 0.9 respectively. It is observed that increasing m and p increases P as expected. The remaining 3 graphs show how P evolves with increasing number of buildings in violation.
The top-right graph (n=40) shows that for P to reach at least 90% with p at 0.7 the inspectors must visit at least 32 sites. Alternatively, when p is 0.9, inspecting 24 sites is sufficient.
Conclusion
In the previous section, we have determined P from a range of values of n,m and p . For the UN, the best scenario is to have unlimited access to every one of North Korea’s nuclear (weapons) sites although the situation considered above is for the limited number of inspections. In the latter case, one can envisage North Korea trying to deceive a group of inspectors by luring them into a dummy site. This will result in a wasted effort leaving one less number of m. It is not hard to imagine discussions ensuing over the value of m between the international community and North Korea at the negotiating table. If it so happens that North Korea categorically refuses to allow inspection of a particular site, then this site is not among N and our equation for P cannot be applied. In this case, the inspection should be stopped as it is pointless to continue without it, and sanctions should remain. As for p, the probability of correctly identifying a violation, many factors contribute to it. The groups of inspectors should be certainly competent and skilled in their areas of expertise so that they do not miss any evidence of violation. However, their physical conditions, such as fatigue, can affect their performance, and their numbers matter as well. As noted, there are only 300 inspectors at the IAEA.
More inspections and better identification of violations (i.e., higher values of m and p) will increase P, the probability of detecting at least one violation. However, the exact value of P remains unknown as n cannot be pre-determined.15 In practical terms, this calls for better intelligence to detect production facilities such as a uranium enrichment plant buried deep underground and good detective work on the part of inspectors. Our example has confirmed our common belief through the use of a mathematical model and illustrated a way of measuring the effectiveness of inspection.
This study reminds us of an Old Russian proverb, ”Trust but verify,” which former U.S. President Ronald Reagan liked quoting in the context of nuclear weapons and arms control with the Soviet Union. In our context, it might be more suitable to say ”Mistrust and verify” judging by North Korea’s past behaviors and untrustworthiness.
Appendix: Inspection Violation (Confidence) Model
Suppose that there are altogether N detected disturbances16 among which n are violations and suppose m≤n inspections are allowed. Let p be the probability of correctly identifying a violation. Then, P denotes the probability that M or more violations are detected, given by the equation below.17
The mathematical terms in the first summation work out the number of ways in which violating and non-violating sites can be chosen in a sample (i.e., m), while the terms in the second summation describe how successfully the inspectors can identify a violating site to be indeed violating. They are recognized as the binomial probability formula. Here,  denotes a binomial coefficient. For the equation to be valid, the following three constraints should hold. First, M≤m as one cannot find more violation(s) than the number of inspections allowed. Second, n≤N as n is simply taken to be violations among N. Third, m≤n as
denotes a binomial coefficient. For the equation to be valid, the following three constraints should hold. First, M≤m as one cannot find more violation(s) than the number of inspections allowed. Second, n≤N as n is simply taken to be violations among N. Third, m≤n as  is mathematically undefined for the case m > n.18
is mathematically undefined for the case m > n.18
It is also assumed that there is at least one violation (i.e., n ≥ 1). The case in which there is no violation (i.e., n = 0) is not of much interest. Also, when considering the lower limit for M, the issue that is of critical importance is whether there is actually a violation or not. The actual number of violations is of secondary importance. Hence, the lower limit for M is set to 1. P is now defined to be the probability of detecting one or more violations, and this definition is used throughout our study. There should be no confusion between P and p, as the latter directly represents such measure as how skilled and competent the inspectors are in detecting a violation once they are at a violating site.
The views expressed herein do not necessarily reflect the views of the Asan Institute for Policy Studies.
- 1. The US State Department has recently used the expression “Final, Fully-Verified Denuclearization” instead of “Complete, Verifiable and Irreversible Dismantlement.” This sounds less provocative to North Korea particularly with the missing word ‘Irreversible.’
- 2. The oversight body consists of representatives from the United States, the United Kingdom, France, Germany, Russia, China and Iran.
- 3. Blaise Misztal, “Iran Deal Limits Inspectors’ Access to Suspicious Sites,” Bipartisan Policy Center, 17th July 2015.
- 4. Timothy Bonds, Eric Larson, Derek Eaton, Richard Darilek, “Strategy-Policy Mismatch, How the U.S. Army Can Help Close Gaps in Countering Weapons of Mass Destruction,” RAND report, 2014.
- 5. “What are N.Korea’s Nuclear Facilities?” The Chosunilbo, 5th May 2018.
- 6. “The Nine Steps Required to Really Disarm North Korea,” The New York Times, 11th June 2018.
- 7. The IAEA, https://www.iaea.org/newscenter/news/new-application-increases-efficiency-and-effectiveness-of-safeguards-verification
- 8. “North Korea has increased nuclear production at secret sites, say U.S. officials,” NBC News, 1st July 2018.
- 9. An inspection process can begin only after receiving a list of nuclear sites declared by North Korea. It is quite another matter whether it will provide a full list.
- 10. Work is in progress to extend the limited scope of the model’s current applications through a different mathematical technique. More extensive work is planned for publication.
- 11. In fact, North Koreans would be foolish to leave any evidence of violation in such a well-known nuclear complex like Yongbyon.
- 12. We are not concerned here about the impact of changing one of n,m or p while the rest remains fixed.
- 13. When it comes to hiding its nuclear warheads, North Korea is unlikely to put all its eggs in one basket. There will be a trade-off between a need to minimize the risk of being detected by storing its warheads in fewer sites as possible and a need to store its warheads in multiple sites to minimize the risk of all its warheads being detected.
- 14. The number of inspections is obtained by dividing n by 5, and then multiplying this number with an integer up to 5.
- 15. We do not know for sure the exact value for the number of nuclear (weapons) sites, N, either.
- 16. This can be simply the number of known nuclear sites such as the number of buildings or facilities rather than the number of disturbances detected. This would depend on the context.
- 17. “Mathematical Models of Arms Control and Disarmament” Application of Mathematical Structures in Politics, Thomas Saaty, John Wiley & Sons, Inc, 1968.
- 18. One can recognize this third constraint as the limitation of the equation P. This is rather restrictive.

 Facebook
Facebook Twitter
Twitter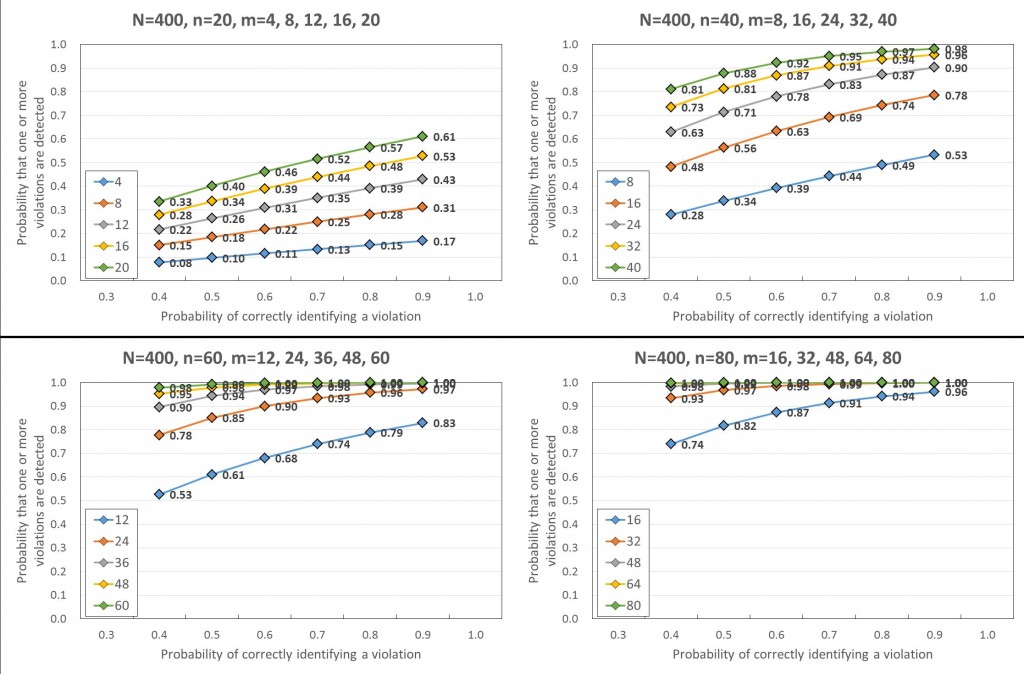
![[Issue Brief] Quantifying the Effectiveness of Nuclear Inspection in North Korea.](http://en.asaninst.org/wp-content/uploads/2018/07/Issue-Brief-Quantifying-the-Effectiveness-of-Nuclear-Inspection-in-North-Korea..jpg)

